In our previous essay, we introduced the concept of predictive processing. The key takeaway from that article is that our brains don’t have direct access to the outside world, therefore they must construct an internal model of it using the imperfect information gathered by our senses. We use this model to make predictions, and when our predictions don’t match what we observe, we call this a prediction error. Our brains can then use these prediction errors to revise our model.1 Simply put, when we make mistakes, we change our minds, or at least we ought to.
But how do we practically apply predictive processing to the way in which we perceive the world around us and update our understandings? That’s what we’ll focus on in this essay: updating our beliefs based on evidence using Bayesian reasoning. In other words, updating our predictions based on our prediction errors by using a simple mathematical theorem called Bayes’ Theorem. But first, let us introduce the problem of focus, which we will use to illustrate Bayesian reasoning…
One of us has a friend named Kevin, yes, that’s his real name. Kevin believes that a New Zealander named Ken Ring, aka the Moonman, can predict long-range weather events by using ‘lunar patterns and astrological techniques.’ To the authors of this article, this sounds very unlikely, although not impossible. To Kevin, it seems likely as he can recall instances of the Moonman being right before.

Long-range weather forecasts tend not to be very accurate because of limitations in the predictive power of weather models beyond a few days out. We don’t know the precise location of every cloud or the precise temperature gradient between every system, so uncertainties are a given. If Moonman’s methods—which supposedly involve analyzing lunar cycles and other natural indicators to make long-range forecasts—were reliable, this would have massive implications.
The New Zealand taxpayer subsidized meteorological services by tens of millions of dollars,this pales in comparison to the US taxpayer subsidies running into the billions. If Moonman’s predictions are accurate, we could just buy one of his one-year daily predictions for the price of only NZ$198.95. In the USA, you would have to buy a prediction for your own area, although at US$125.19 for Los Angeles, it would be a bargain at twice the price.2

We the authors have a model of reality that doesn’t include using the moon to predict weather, while our friend Kevin does.3 Either our model of reality is wrong, or Kevin’s is wrong. There’s also a third option: everyone is wrong. But how would we know? Fortunately, the Moonman has made predictions. By comparing the accuracy of the Moonman’s predictions with established meteorological data, we can objectively assess the validity of his methods. If we are right, then the predictions won’t be accurate, and if Kevin is right, they will be.
This sets up a perfect opportunity to use Bayesian reasoning to test our models of reality. Bayesian reasoning, named for the 17th century mathematician Thomas Bayes, is a statistical method we can use to update our beliefs based on new evidence. We start with an initial belief (or “prior”) about something, and then we receive new information (or “evidence”). Bayesian reasoning helps us combine our prior beliefs with the new evidence to form an updated belief (or “posterior”).
If you’d like a deeper explanation of the mathematical theorem behind Bayesian Reasoning, check out this video: Bayes theorem, the geometry of changing beliefs by Three Blue One Brown
A single correct prediction typically doesn’t prove anything definitively, and a single prediction error typically doesn’t disprove anything either. Instead, they help us revise our positions or credence. As we incrementally gather more evidence, each accurate prediction by the Moonman would increase our credence in his methods, while each inaccurate prediction would decrease it. Over time, this process helps us refine our internal models of reality.
With each new piece of evidence, we must ask ourselves: could this evidence be observed if we are wrong?
It’s worth noting that most of the time, the predictive processing abilities of our brain are functioning subconsciously, which is especially evident to those of you who this is all new to. Our brains are predictive processing machines and they will continue to be without our conscious effort. However, understanding predictive processing and the way that Bayesian reasoning works can help us deliberately become better critical thinkers.
Now back to the weather…
Before we can apply Bayesian reasoning to try and resolve our disagreement about the Moonman, we need to set some ground rules. First, we have to be explicit about what is the claim and counterclaim under investigation. In this case, the claim is that the Moonman’s long-term weather predictions are reliable. This means the counterclaim becomes: the Moonman’s long-term weather predictions are not reliable.
The next step is for all parties concerned to state their credence in the claim under investigation, that is, the extent to which they trust the claim, ranging from 0 to 100%.
Luke is new to the claim about Moonman’s ability to predict the weather, he thinks it’s unlikely but not impossible. His credence is around 10%. Kevin, on the other hand, recalls the Moonman’s predictions being right before, Kevin’s credence is around 80%. Zafir is very skeptical as he has read articles that are very critical of the Moonman, his credence is at 0.05%.
With our initial credences stated, we must agree on what we should do with our positions as new evidence comes to light. With each new piece of evidence, we must ask ourselves: could this evidence be observed if we are wrong? This is actively pushing back against confirmation bias and is perhaps one of the most important questions a critical thinker can ask themselves. This question unlocks the key insight behind Bayesian Reasoning, which compares the likelihood of observing evidence if the claim is correct to the likelihood of observing the same evidence if the claim is incorrect.
The philosopher Andy Norman put forward a concept that he called Reason’s Fulcrum.4 The idea of weighing up evidence for and against a claim, or making a pros and cons list for an important decision, is familiar to most people. We can visualize this as a simple lever or scale. When the weight of evidence or reason is more on one side than the other, we should revise our beliefs to match.
A simple lever has two parts: the beam, which can be any rigid object that will hold up under force, and the fulcrum, which sits under the beam and provides a point to pivot on. In Andy’s framing, the fulcrum represents our willingness to change our minds. It is the willingness to yield to better reasons or evidence. This willingness to yield to better reasons or evidence is crucial. Without it, the force of reason and evidence cannot gain the leverage required to shift our beliefs. Andy goes as far as to call this an obligation that a person must have to be considered reasonable.
But what if the fulcrum is damaged? Emotional attachment to a belief or identifying too strongly with it can make us resistant to change. When we become invested in a belief, it becomes difficult to remain open to new evidence that contradicts it. This attachment can damage Reason’s Fulcrum, undermining our ability to treat reason and evidence fairly.
Reason’s Fulcrum Infographic on the CIRCE website
It’s a good analogy, although it’s not quite Bayesian. There are two small adjustments required for Reason’s Fulcrum to become an accurate representation of Bayesian reasoning. First, the fulcrum needs to be moveable according to our prior credence, or our confidence in the claim being investigated. So we have the claim on the right-hand side and the counterclaim on the left, and the position of the fulcrum represents our position on the claim.
For Luke his 10% credence becomes 0.1 of the way along the beam, the fulcrum is closer to the counterclaim (Moonman’s predictions are not reliable), because that’s what he thinks is more likely. Kevin's 80% becomes, or 0.8 of the way along the beam. His fulcrum is closer to the claim as he thinks it’s probably true that the Moonman can predict the weather.
Zafir’s extremely skeptical credence of 0.05% becomes 0.0005 along the beam, or thinking there is only a 1 in 2,000 chance that the claim is correct.
What this means is that Luke would require some good evidence, or atleast a good amount of evidence to think that this claim about Moonman’s ability to predict long range weather is probably true. Kevin, who already has a high prior credence in the claim will need quite significant counter evidence to reduce his belief in the claim. Any evidence for the claim would strengthen his belief in it. As Zafir thinks the claim is extraordinarily unlikely, he would require either extraordinary evidence or at least many lines of ordinary evidence.
The second crucial and nuanced difference between a person who employs Bayesian reasoning is that evidence doesn’t add up to make something more likely. With each new piece of evidence, the Bayesian thinker refines and changes how likely they think something is. In effect, it makes the alternative look less likely. Each piece of evidence doesn’t get applied to the end of the lever due to which claim it looks like it supports. Instead, it is applied due to the likelihood of observation given the claim and the counterclaim.
That’s the nuanced thing about Bayesian reasoning: how to think about evidence doesn’t just involve whether the prediction was correct, but also how likely that prediction was given the context.

For example, correctly predicting rain for Auckland on a day in October is not strong evidence. On average, it rains on 17 days in Auckland during October.5 This correct prediction won’t significantly increase our credence in the Moonman’s methods because the prediction was not particularly surprising. It’s not a glaring error signal in their worldviews. However, if the Moonman predicted an unusual event with a great deal of accuracy, then this would be more likely to be observed if Kevin’s worldview was more accurate than ours. Conversely, if the Moonman consistently predicts weather events that do not occur, this should decrease Kevin’s credence in his position on the claim.
The mathematics of Bayes expressed in this way is rather simple. We take our credence in the claim and multiply it by the likelihood of observing the evidence given the claim, and do the same for the counterclaim. For example, let’s look at Luke's position on the Moonman’s ability to predict the weather. His 10% credence means he thinks there is a 1 in 10 chance that the Moonman is on to something. That means his fulcrum is set at a ratio of 1 to 9. This is 1 for the claim (can reliably predict the weather) and 9 for the counterclaim (cannot reliably predict the weather).
But what if the Moonman correctly predicted something more unusual and specific, such as a heavy rainfall event for Auckland on the 15th of October. Heavy rainfall events are when there is more than 100 mm (about 4 inches) of rain in less than 24 hours. These events occur about 7 days a year in Auckland,6 so for simplicity’s sake, let's say the odds are 1 in 50. Therefore, the probability of observing the evidence (a heavy rainfall event) under the counterclaim (the Moonman cannot reliably predict the weather) is about 1 in 50, or 2%. This is what we would expect to see even if the claim about the reliability of the Moonman’s predictions was false. For the probability of observing the evidence given the claim, we will assign 90%. This is mostly subjective, as this is the kind of thing we would expect to see if he could accurately predict the weather.
When it comes to assigning a probability to observing evidence in support of a claim, we don’t assign 100% because a single incorrect prediction would disprove the claim under investigation, and we don’t assign 50% or lower because a correct prediction would not significantly increase our confidence, it may even lower it. It matters less what our subjective allocations are, provided we apply the same standards to each new line of evidence that comes in. A higher probability assigned to observing the prediction given the claim will have a larger impact on our confidence given a correct prediction, but will also mean a larger reduction in our confidence given an incorrect prediction.
This is a very important concept: how we respond to evidence is heavily influenced by how likely we think the claim is before we start.
So, given this correct prediction of heavy rainfall by the moonman, on Luke’s Fulcrum, this becomes 1 x 90% for the claim and 9 x 2% for the counterclaim. This works out to 0.9 to 0.18, which is a ratio of 5 to 1 or, in terms of credence for the claim, 83%. Luke’s fulcrum would get a large reset from 0.1 of the way along the beam to 0.83 of the way along the beam.
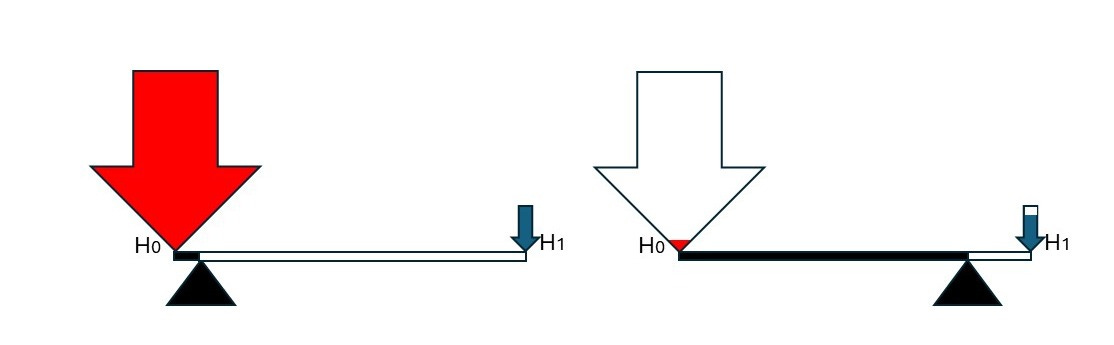
If Moonman’s prediction failed (there isn’t a heavy rainfall event on the 15th of October) then the calculation becomes 1 x 10% for the claim (10% representing the probability of not observing evidence in support of the claim, the complement of 90%) and 9 x 98% for the counterclaim (98% being the complement of 2%) resulting in Luke reducing his credence in the Moonman’s abilities all the way down to 1.1%.
If the Moonman’s heavy rainfall prediction was correct, for Kevin, at an initial 80% credence, his credence would go up to 94.7%. The movement of his fulcrum would look like this: 8 x 90% for the claim and 2 x 2% for the counterclaim, for a new ratio of 18 to 1 (18/19=94.7%). If the Moonman’s prediction was wrong then Kevin should revise his credence down to 29% (8 x 10% compared to 2 x 98%).
For Zafir it looks a little different, even a compelling piece of evidence, such as an accurate prediction of a heavy rainfall event, would not make Zafir a believer, and this is appropriate as he thought it was extremely unlikely to begin with and the new evidence could be observed if the claim was false. Still, his fulcrum would move from his prior position of 0.0005 of the way along the beam to about 0.02 of the way along the beam, 0.05% to 2%.
This is a very important concept: how we respond to evidence is heavily influenced by how likely we think the claim is before we start. Although the encouraging thing is that we would all move in the same direction, and as new lines of evidence come to light, our positions will eventually fine-tune towards what is more likely to be true. If, for example, the Moonman’s next 5 predictions were to all fail, all three of our positions would converge near the counterclaim.
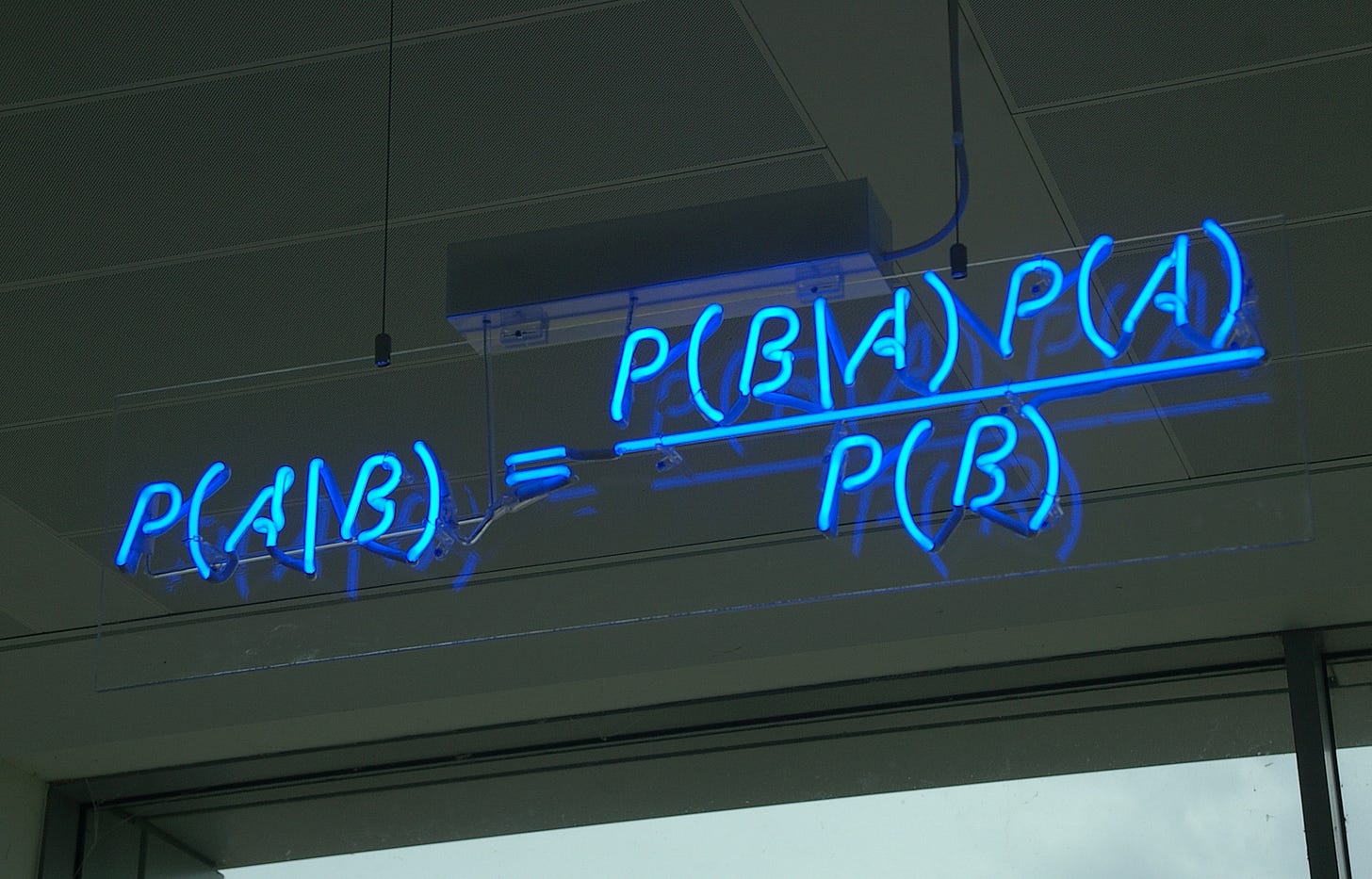
We are not recommending that you perform such calculations whenever you are confronted by evidence for or against a claim, but we do hope that you consider how the principles of Bayesian reasoning can roughly apply to the way in which you change your mind in light of new evidence.
Our preexisting credence in claims alters how much we are swayed by evidence, and this is entirely appropriate. What isn’t appropriate is if our position is one of unwavering faith in a preexisting belief, then we become resistant to counterevidence. It’s like we are operating without a fulcrum. We become unable to ask ourselves “Could this evidence be observed if I’m wrong?” If we are not asking ourselves that question, then are we trying to fit our worldview to the evidence or are we trying to fit the evidence to our worldview?
Thanks for reading. There’s more to come. 😁
If you got lost in the math above, we recommend watching this great explanation by the public thinker and author, Julia Galef, which very effectively explains the utility of Bayesian Reasoning: Julia Galef: Think Rationally via Bayes' Rule | Big Think.
But, if you’d like to learn more about the mathematical side of Bayesian reasoning, in addition to the video linked earlier in the essay, this page on Bayes’s Theorem from Angelo's Math Notes also explains Bayes’ Theorem very well. This page from Better Explained is also great explanation: An Intuitive (and Short) Explanation of Bayes’ Theorem
Did you find any errors in this essay? If so, please email Luke at luke@cognitiveimmunolgy.net. Or, if you’re receiving this post in your inbox, simply respond to the email.
The predictions we're talking about are not the typical sort of predictions that we consciously make but unconscious expectations. When these unconscious expectations are violated the resulting prediction errors do, however, often manifest as a conscious experience of surprise.
It’s worth noting, for the sake of scientific accuracy, the moon does seem to have an extremely minor influence on weather patterns. See this BBC article. “Researchers at the University of Washington reported that lunar forces do affect the amount of rainfall – but only by around 1%.”
Norman, A. (2021). Mental immunity: Infectious ideas, mind-parasites, and the search for a better way to think. HarperCollins. https://andynorman.org/mental-immunity/
It’s worth noting that Andy is the founder and director of CIRCE, the nonprofit parent organization of the Mental Immunity Project.






